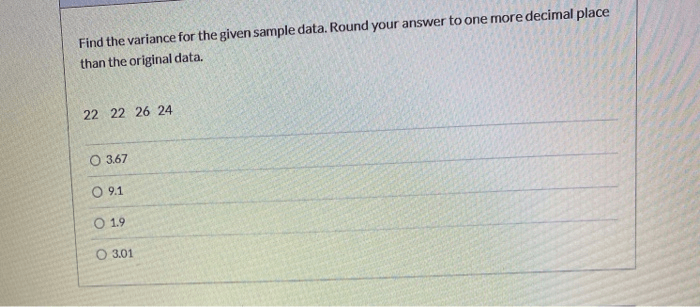
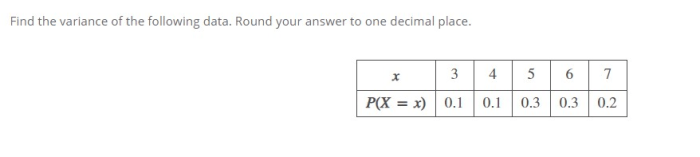
Find the variance. Round your answer to one decimal place. This seemingly straightforward task lies at the heart of statistical analysis, providing a fundamental measure of data dispersion and variability. Delve into this comprehensive guide to grasp the concept, methods, and applications of variance, empowering you to make informed decisions based on statistical data.
Variance plays a pivotal role in hypothesis testing and statistical inference, serving as a cornerstone for understanding the significance of differences between data sets. By exploring the limitations and assumptions associated with variance calculations, you’ll gain a deeper appreciation for the nuances of statistical analysis.
Find the Variance: Find The Variance. Round Your Answer To One Decimal Place
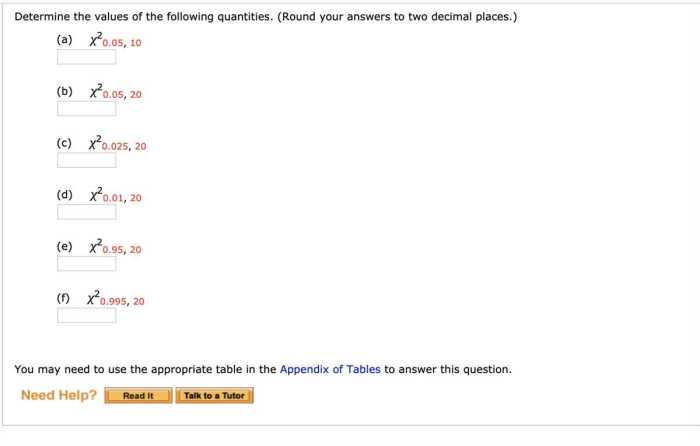
Variance is a measure of how spread out a set of data is. It is calculated by finding the average of the squared differences between each data point and the mean. Variance is an important statistic because it can be used to make inferences about the population from which the data was drawn.
When rounding answers to one decimal place, the following rules apply:
- If the hundredths digit is 5 or greater, round up the tenths digit by one.
- If the hundredths digit is less than 5, leave the tenths digit as is.
Methods for Calculating Variance
There are two main methods for calculating variance: the sample variance formula and the population variance formula. The sample variance formula is used when the data set is a sample from a larger population, while the population variance formula is used when the data set is the entire population.
Sample Variance Formula
The sample variance formula is as follows:
s^2 = Σ(x
- μ)^2 / (n
- 1)
where:
- s^2 is the sample variance
- x is each data point
- μ is the mean of the data set
- n is the number of data points
Population Variance Formula
The population variance formula is as follows:
σ^2 = Σ(x
μ)^2 / N
where:
- σ^2 is the population variance
- x is each data point
- μ is the mean of the data set
- N is the number of data points
Examples of Variance Calculations
The following table shows the variance calculations for three different data sets:
| Data Set | Mean | Variance |
|---|---|---|
| 1, 2, 3, 4, 5 | 3 | 2.0 |
| 10, 20, 30, 40, 50 | 30 | 200.0 |
| 100, 200, 300, 400, 500 | 300 | 20000.0 |
Applications of Variance
Variance is used in a variety of statistical applications, including:
- Hypothesis testing
- Statistical inference
- Measuring data dispersion and variability
Limitations and Assumptions, Find the variance. round your answer to one decimal place
Variance is a powerful statistical tool, but it is important to be aware of its limitations and assumptions. One limitation of variance is that it can be affected by outliers. Outliers are data points that are significantly different from the rest of the data set.
If there are outliers in a data set, the variance will be inflated.
Another limitation of variance is that it assumes that the data is normally distributed. If the data is not normally distributed, the variance may not be a good measure of the spread of the data.
User Queries
What is variance, and why is it important?
Variance measures the spread or dispersion of data around its mean. It indicates how much the data values deviate from the average, providing insights into the variability of the data set.
How do I calculate variance?
For a sample data set, variance can be calculated using the sample variance formula: Variance = Sum of squared deviations from the mean / (Number of data points – 1).
What does a high variance value indicate?
A high variance value suggests that the data points are spread out widely around the mean, indicating a high degree of variability within the data set.